十大算法

一、二分查找（非递归）

1、非递归二分查找概述

二分查找法只适用于从有序的数列中进行查找(比如数字和字母等)，将数列排序后再进行查找
二分查找法的运行时间为对数时间 O(㏒₂n)，即查找到需要的目标位置最多只需要㏒₂n 步

2、非递归二分查找代码实现

java

package work.rexhao.search;

/**
 * 非递归二分查找
 *
 * @author 王铭颢
 * @Date 2022/7/14 11:05
 */
public class BinarySearchNoRecursion {
    public static void main(String[] args) {
        int[] num = new int[]{10, 12, 23, 32, 45, 64, 65, 69, 83};
        System.out.println(binarySearchNoRecursion(10, num));
        System.out.println(binarySearchNoRecursion(65, num));
        System.out.println(binarySearchNoRecursion(99, num));
    }

    public static int binarySearchNoRecursion(int target, int[] num) {
        int left = 0;
        int right = num.length - 1;
        int mid;
        while (left <= right) {
            mid = (left + right) / 2;
            if (target == num[mid]) {
                return mid;
            } else if (target > num[mid]) {
                // 目标值比中间值大 --> 向右找
                left = mid + 1;
            } else {
                // 目标值比中间值小 --> 向左找
                right = mid - 1;
            }
        }
        return -1;
    }
}

3、补：递归二分查找代码实现

java

package work.rexhao.search;

import java.util.Arrays;

/**
 * 二分查找
 *
 * @author 王铭颢
 * @Date 2022/7/3 22:54
 */
public class BinarySearch {
    public static void main(String[] args) {
        int[] num = new int[]{10, 12, 23, 32, 45, 64, 65, 69, 83};
        System.out.println(Arrays.toString(num));
        System.out.println(binarySearch(num, 69, 0, num.length - 1));
        System.out.println(binarySearch(num, 99, 0, num.length - 1));
    }

    public static int binarySearch(int[] num, int target, int left, int right) {
        if (left > right) {
            return -1;
        }
        if (num[(left + right) / 2] == target) {
            return (left + right) / 2;
        } else if (num[(left + right) / 2] > target) {
            return binarySearch(num, target, left, (left + right) / 2);
        } else {
            return binarySearch(num, target, (left + right) / 2 + 1, right);
        }
    }
}

二、分治算法（DC）

1、分治算法介绍

分治法（Divide-and-Conquer(P)）是一种很重要的算法。

字面上的解释是“分而治之”，就是把一个复杂的问题分成两个或更多的相同或相似的子问题，再把子问题分成更小的子问题……直到最后子问题可以简单的直接求解，原问题的解即子问题的解的合并。

2、分治算法的基本步骤

分解：将原问题分解为若干个规模较小，相互独立，与原问题形式相同的子问题
解决：若子问题规模较小而容易被解决则直接解，否则递归地解各个子问题
合并：将各个子问题的解合并为原问题的解

3、分治算法设计模式

java

if |p| <= n0
	then return(ADHOC(P))
// 将p分解为较小的子问题p1,P2,…,Pk
for if <- 1 to k
do yi <-  DC递归解决pi
T <- MERGE(y1,x2,…,vk) 合并子问题
return(T)

其中|P|表示问题p的规模
n0为一國值，表示当问题P的规模不超过no时，问题已容易直接解出，不必再继续分解。
ADHOC(P)是该分治法中的基本子算法，用于直接解小规模的问题P。因此，当P的规模不超过n0时直接用算法ADHOC(P)求解。
算法MERGE(y1,x2,…,vk)是该分治法中的合并子算法，用于将P的子问题p1,p2,…,pk的相应的解y1,x2,…,vk合并为P的解。

4、汉诺塔代码实现

java

package work.rexhao.algorithm.dc;

import java.util.Collections;

/**
 * 汉诺塔
 *
 * @author 王铭颢
 * @Date 2022/7/14 10:10
 */
public class hanoiDemo {
    static int count = 0;

    public static void main(String[] args) {
        hanoiTower(5, 'A', 'B', 'C');
    }

    private static void hanoiTower(int num, char a, char b, char c) {
        // 如果只有一个盘
        if (num == 1) {
            System.out.println(++count + " : 第 1 个盘从 " + a + "->" + c);
        } else {
            // 如果我们有 n >= 2 情况，我们总是可以看做是两个盘 1.最下边的一个盘 2. 上面的所有盘

            // 1. 先把 最上面的所有盘 A->B， 移动过程会使用到 c
            hanoiTower(num - 1, a, c, b);

            // 2. 把最下边的盘 A->C
            System.out.println(++count + " : 第 " + num + " 个盘从 " + a + "->" + c);

            // 3. 把 B 塔的所有盘 从 B->C , 移动过程使用到 a 塔
            hanoiTower(num - 1, b, a, c);
        }
    }
}

三、动态规划（DP）

1、动态规划算法介绍

动态规划（Dynamic Programming）算法的核心思想是：将大问题划分为小问题进行解决，从而一步步获取最优解的处理算法
动态规划算法与分治算法类似，其基本思想也是将待求解问题分解成若干个子问题，先求解子问题，然后从这些子问题的解得到原问题的解。
与分治法不同的是，适合于用动态规划求解的问题，经分解得到子问题往往不是互相独立的。（即下一个子阶段的求解是建立在上一个子阶段的解的基础上，进行进一步的求解）
动态规划可以通过填表的方式来逐步推进，得到最优解。

2、背包问题

1）背包问题概述

有一个背包，容量为4kg，现有如下物品。要求达到的目标为装入的背包的总价值最大，并且重量不超出装入的物品不能重复。

物品	重量	价值
G	1	15
S	4	30
L	3	20

2）背包问题思路分析

背包问题主要是指一个给定容量的背包、若干具有一定价值和重量的物品，如何选择物品放入背包使物品的价值最大。其中又分 01 背包和完全背包（完全背包指的是：每种物品都有无限件可用，且无限背包可以转化为 01 背包）

算法的主要思想，利用动态规划来解决。每次遍历到的第 i 个物品，根据 w[i]和 v[i]来确定是否需要将该物品放入背包中。即对于给定的 n 个物品，设 v[i]、w[i]分别为第 i 个物品的价值和重量，C 为背包的容量。再令 v[i][j]表示在前 i 个物品中能够装入容量为 j 的背包中的最大价值。

v[i][0]=v[0][j]=0; 表示填入表第一行和第一列是 0
当 w[i]> j ：v[i][j]=v[i-1][j] 当准备加入新增的商品的容量大于当前背包的容量时，就直接使用上一个单元格的装入策略
当 j>=w[i]时：v[i][j]=max{v[i-1][j], v[i]+v[i-1][j-w[i]]} 当准备加入的新增的商品的容量小于等于当前背包的容量,
装入的方式:
1. v[i-1][j]：就是上一个单元格的装入的最大值
2. v[i] ：表示当前商品的价值
3. v[i-1][j-w[i]] ：装入 i-1 商品，到剩余空间 j-w[i]的最大值
4. 当 j>=w[i]： v[i][j]=max{v[i-1][j], v[i]+v[i-1][j-w[i]]} :

3）背包问题代码实现

java

package work.rexhao.algorithm.dynamic;

/**
 * 01背包问题
 *
 * @author 王铭颢
 * @Date 2022/7/14 10:07
 */
public class KnapsackProblem {
    public static void main(String[] args) {
        // 1. 定义二维数组
        int knapsackSize = 4;    // 背包容量
        int goodsType = 3;  // 物品种类
        int[][] value = new int[knapsackSize + 1][goodsType + 1];   // dp价值表
        int[] goodsSize = {0, 1, 4, 3};    // 每个物品的大小
        int[] goodsValue = {0, 15, 30, 20};  // 每个物品的价值

        // 2. 第一行为空（空背包）且第一列为空（背包容量为0）

        // 3. 遍历表
        for (int i = 1; i < knapsackSize + 1; i++) {
            // i:背包容量
            for (int j = 1; j < goodsType + 1; j++) {
                // j:物品类型
                knapsackProblem(knapsackSize, i, j, value, goodsSize, goodsValue);
            }
        }

        // 3.1 打印表
        for (int i = 0; i < goodsType + 1; i++) {
            for (int j = 0; j < knapsackSize + 1; j++) {
                System.out.print(value[j][i] + "\t");
            }
            System.out.println();
        }
        System.out.println("--------------------");

        // 4. 输出答案
        int ans = 0;
        for (int[] ints : value) {
            for (int i : ints) {
                ans = Math.max(ans, i);
            }
        }
        System.out.println("总价值最大为: " + ans);
    }

    private static void knapsackProblem(int knapsackSize, int i, int j, int[][] value, int[] goodsSize, int[] goodsValue) {
        if (goodsSize[j] == i) {
            // 放一个正好放满 --> 放(这个或上一个品种)中价值更高的
            value[i][j] = Math.max(goodsValue[j], value[i][j - 1]);
        } else if (goodsSize[j] > i) {
            // 这个放不下 --> 放上一品种的
            value[i][j] = value[i][j - 1];
        } else {
            // 放下了，但是剩下位置了 --> 剩下位置找本行相应的那个 --> 放(这个或上一个品种)中价值更高的
            value[i][j] = Math.max(goodsValue[j] + value[i - goodsSize[j]][j], value[i][j - 1]);
        }
    }

}

/*
    问题：有一个背包，容量为 4kg， 现有如下物品
         要求达到的目标为装入的背包的总价值最大，并且重量不超出
    G   1kg     15
    S   4kg     30
    L   3Kg     20
 */

3、最少步数问题

1）最少步数问题概述

河上有一排n个荷叶（编号依此为1,2,3····n），第i个荷叶上有一个整数ai，现在有一只小青蛙在第1个荷叶上，荷叶上的整数表示小青蛙在该位置可以向前跳跃最多的荷叶个数。求小青蛙从第1个荷叶跳到第n个荷叶用的最少的步数为小饼干的考试次数。

https://ac.nowcoder.com/acm/contest/25592/F

2）最少步数问题思路分析

建立step[]数组，存放到达相应位置最少的步数

3）最少步数问题代码实现

java

import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        int[] step = new int[n + 1];
        for (int i = 1; i <= n; i++) step[i] = 99999;
        step[1] = 0;
        for (int i = 1; i <= n; i++) {
            int t = sc.nextInt();
            for (int j = 1; j <= t; j++) {
                if (i + j > n) continue;
                step[i + j] = Math.min(step[i + j], step[i] + 1);
            }
        }
        System.out.println(step[n]);
    }
}

四、KMP算法

1、字符串匹配问题

有一个字符串 str1 = "i love java do you like java"，和一个子串 str2 ="java"

现在要判断 str1 是否含有 str2。如果存在，就返回第一次出现的位置。没有则返回-1。

2、暴力破解（BF）代码实现

java

package work.rexhao.algorithm.KMP;

/**
 * 字符串匹配问题暴力破解
 *
 * @author 王铭颢
 * @Date 2022/7/14 11:12
 */
public class BF {
    public static void main(String[] args) {
        String str1 = "i love java do you like java";
        String str2 = "java";
        System.out.println(bf(str1, str2));
    }

    private static int bf(String str1, String str2) {
        int len1 = str1.length();
        int len2 = str2.length();
        for (int i = 0; i < len1; i++) {
            int temp = i;
            for (int j = 0; j < len2; j++) {
                if (str1.charAt(i) == str2.charAt(j)) {
                    i++;
                    if (j == len2 - 1) {
                        return temp;
                    }
                } else {
                    i = temp;
                    break;
                }
            }
        }
        return -1;
    }
}

3、KMP介绍

字符串查找算法（Knuth-Morris-Pratt），简称为 “KMP 算法”，常用于在一个文本串 S 内查找一个模式串 P 的出现位置，这个算法由 Donald Knuth、Vaughan Pratt、James H. Morris 三人于 1977 年联合发表，故取这 3 人的姓氏命名此算法
KMP 方法算法就利用之前判断过信息，通过一个 next 数组，保存模式串中前后最长公共子序列的长度，每次回溯时，通过 next 数组找到，前面匹配过的位置，省去了大量的计算时间

4、KMP思路分析

...

5、KMP代码实现

java

package work.rexhao.algorithm.KMP;

import java.util.Arrays;

/**
 * KMP算法
 *
 * @author 王铭颢
 * @Date 2022/7/15 19:56
 */
public class KMP {
    public static void main(String[] args) {
        String str1 = "BBC ABCDAB ABCDABCDABDE";
        String str2 = "ABCDABD";

        System.out.println(kmpSearch(str1, str2));
    }

    public static int[] kmpNext(String target) {
        int[] next = new int[target.length()];
        next[0] = 0;
        int j = 0;
        for (int i = 1; i < target.length(); i++) {
            if (target.charAt(i) == target.charAt(j)) {
                j++;
            } else {
                if (j > 0) {
                    j = next[j - 1];
                }
            }
            next[i] = j;
        }
        return next;
    }

    public static int kmpSearch(String str1, String str2) {
        int[] next = kmpNext(str2);
        int j = 0;
        for (int i = 0; i < str1.length(); i++) {
            if (str1.charAt(i) == str2.charAt(j)) {
                j++;
            } else {
                if (j > 0) {
                    j = next[j - 1];
                }
            }
            if (j == str2.length()) {
                return i - j + 1;
            }
        }
        return -1;
    }
}

五、贪心算法

1、贪心算法介绍

贪婪算法（贪心算法）是指在对问题进行求解时，在每一步选择中都采取最好或者最优（即最有利）的选择，从而希望能够导致结果是最好或者最优的算法。

2、集合覆盖问题

假设存在下面需要付费的广播台，以及广播台信号可以覆盖的地区。如何选择最少的广播台，让所有的地区都可以接收到信号

广播台	覆盖地区
K1	"北京", "上海", "天津"
K2	"广州", "天津", "深圳"
K3	"成都", "上海", "杭州"
K4	"上海", "天津"
K5	"杭州", "大连"

目前并没有算法可以快速计算得到准备的值，使用贪婪算法，则可以得到非常接近的解，并且效率高。选择策略上，因为需要覆盖全部地区的最小集合。
遍历所有的广播电台, 找到一个覆盖了最多未覆盖的地区的电台(此电台可能包含一些已覆盖的地区，但没有关系。
将这个电台加入到一个集合中，想办法把该电台覆盖的地区在下次比较时去掉。
重复第 1 步直到覆盖了全部的地区。

贪婪算法所得到的结果不一定是最优的结果(有时候会是最优解)，但是都是相对近似(接近)最优解的结果

3、集合覆盖问题代码实现

java

package work.rexhao.algorithm.greedy;

import java.util.*;

/**
 * 贪心算法
 *
 * @author 王铭颢
 * @Date 2022/7/14 19:58
 */
public class GreedyAlgorithm {
    public static void main(String[] args) {
        /*
            K1  "北京", "上海", "天津"
            K2  "广州", "天津", "深圳"
            K3  "成都", "上海", "杭州"
            K4  "上海", "天津"
            K5  "杭州", "大连"
         */
        String[][] area = {{"北京", "上海", "天津"}, {"广州", "天津", "深圳"},
                {"成都", "上海", "杭州"}, {"上海", "天津"}, {"杭州", "大连"}};
        HashSet<String> allPlace = new HashSet<>();
        HashMap<String, HashSet<String>> map = new HashMap<>();
        for (String[] strs : area) {
            allPlace.addAll(Arrays.asList(strs));
        }
        for (int i = 0; i < 5; i++) {
            map.put("K" + (i + 1), new HashSet<>(Arrays.asList(area[i])));
        }

        ArrayList<String> ansList = new ArrayList<>();
        while (!allPlace.isEmpty()) {
            int maxValue = 0, maxIndex = 0;
            for (int i = 0; i < map.size(); i++) {
                HashSet<String> set = map.get("K" + (i + 1));
                int thisValue = 0;
                for (String s : set) {
                    if (allPlace.contains(s)) thisValue++;
                }
                if (thisValue > maxValue) {
                    maxIndex = i;
                    maxValue = thisValue;
                }
            }

            HashSet<String> maxSet = map.get("K" + (maxIndex + 1));
            for (String s : maxSet) {
                allPlace.remove(s);
            }
            ansList.add("K" + (maxIndex + 1));
        }

        System.out.println(Arrays.toString(ansList.toArray()));
    }

}

六、普利姆算法（Prim）

作者对于二者算法（克鲁斯卡尔算法与普利姆算法）的了解有待提升
代码实现仅供参考

1、最小生成树

最小生成树（Minimum Cost Spanning Tree），简称MST。一个带权的无向连通图，选取一棵使树上所有边上权的总和为最小的生成树。

N个顶点，一定有N-1条边
包含全部顶点
N-1条边都在图中

2、普利姆算法概要

普利姆（Prim）算法求最小生成树，也就是在包含 n 个顶点的连通图中，找出只有(n-1)条边包含所有 n 个顶点的连通子图，也就是所谓的极小连通子图

3、修路问题

有 7 个村庄（A, B, C, D, E, F, G），如何修路保证各个村庄都能连通，并且总的修建公路总里程最短？

修路问题

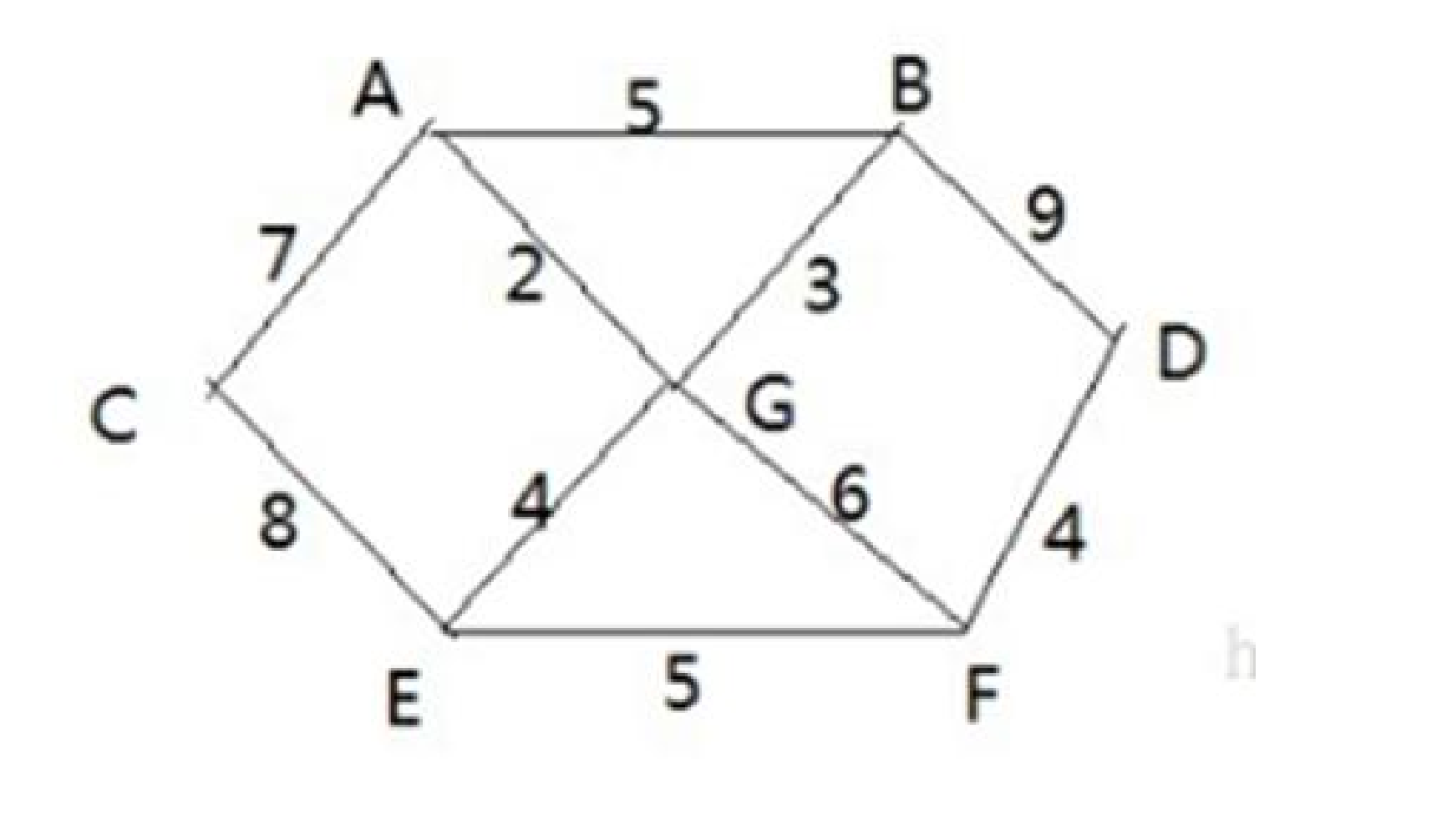
4、普利姆算法代码实现

java

package work.rexhao.algorithm.prim;

import com.sun.xml.internal.bind.v2.schemagen.xmlschema.TypeHost;

import java.util.*;

/**
 * 普利姆算法
 *
 * @author 王铭颢
 * @Date 2022/7/14 21:00
 */
public class PrimAlgorithm {
    public static void main(String[] args) {
        String[] nodeName = {"A", "B", "C", "D", "E", "F", "G"};
        Graph graph = new Graph(7, nodeName);
        System.out.println("最短路径为: " + prim(graph));
    }

    public static boolean isEmpty(boolean[] b) {
        for (boolean B : b) {
            if (!B) {
                return true;
            }
        }
        return false;
    }

    private static int prim(Graph graph) {
        int ans = 0;
        // 找一个开始点 --> A
        boolean[] flag = new boolean[graph.n];
        flag[0] = true;
        // 遍历其他点
        while (isEmpty(flag)) {
            int minValue = 10000;
            int[] minIndex = new int[2];
            for (int i = 0; i < graph.edges.length; i++) {
                for (int j = 0; j < graph.edges[i].length; j++) {
                    if (graph.edges[i][j] == 0) continue;
                    if (flag[i] && !flag[j] && graph.edges[i][j] < minValue) {
                        minValue = graph.edges[i][j];
                        minIndex[0] = i;
                        minIndex[1] = j;
                    }
                }
            }
            flag[minIndex[0]] = flag[minIndex[1]] = true;
            ans += minValue;
        }
        return ans;
    }
}

class Graph {
    int[][] edges;  // 邻接矩阵
    int n;  // 节点个数
    List<String> node;  // 节点名称

    public Graph(int n, String[] nodeName) {
        this.edges = new int[n][n];
        this.n = n;
        this.node = new ArrayList<>(Arrays.asList(nodeName));
        this.init();
    }

    private void init() {
        /*
            "A"     0
            "B"     1
            "C"     2
            "D"     3
            "E"     4
            "F"     5
            "G"     6
         */
        // A-B:5    A-C:7   A-G:2
        add(0, 1, 5).add(0, 2, 7).add(0, 6, 2);
        // F-E:5    F-D:4   F-G:6
        add(5, 4, 5).add(5, 3, 4).add(5, 6, 6);
        // E-G:4    E-C:8
        add(4, 6, 4).add(4, 2, 8);
        // B-D:9    B-G:3
        add(1, 3, 9).add(1, 6, 3);
    }

    public Graph add(int i, int j, int weight) {
        edges[i][j] = edges[j][i] = weight;
        return this;
    }
}

七、克鲁斯卡尔算法（Kruskal）

1、克鲁斯卡尔算法概要

克鲁斯卡尔（Kruskal）算法，是用来求加权连通图的最小生成树的算法。

基本思想：按照权值从小到大的顺序选择 n-1 条边，并保证这 n-1 条边不构成回路

具体做法：首先构造一个只含 n 个顶点的森林，然后依权值从小到大从连通网中选择边加入到森林中，并使森林中不产生回路，直至森林变成一棵树为止

2、Kruskal与Prim的区别

Prim算法是直接查找，多次寻找邻边的权重最小值；Kruskal算法采用贪心策略，是需要先对权重排序后查找的。
Kruskal算法在效率上比Prim算法快，因为Krusal算法只要对所有边排序一次就能找到最小生成树；而Prim算法需要对邻边进行多次排序才能找到。
Prim算法：选择一个顶点作为树的根节点，然后找到以这个点为邻边的最小权重的点，然后将其加入最小生成树中，再重复查找这棵最小生成树的权重最小的边的点，加入其中。(如果加入要产生回路，就跳过这条边)。当所有结点加入最小生成树中，就找到了这个连通图的最小生成树。
Kruskal算法：利用贪心策略，再找最小生成树结点之前，需要对边的权重从小到大排序，将排序好的权重边依次加入到最小生成树中(如果加入时产生回路就跳过这条边，加入下一条边)，当加入的边数为n-1时，就找到了这个连通图的最小生成树。
Prim算法适合边稠密图，时间复杂度O(n²)
Kruskal算法与边有关，适合于稀疏图O(eloge)

3、克鲁斯卡尔算法代码实现

java

package work.rexhao.algorithm.kruskal;

import java.util.ArrayList;
import java.util.Arrays;
import java.util.HashSet;
import java.util.List;

/**
 * 克鲁斯卡尔算法
 *
 * @author 王铭颢
 * @Date 2022/7/14 22:42
 */
public class KruskalAlgorithm {
    public static void main(String[] args) {
        String[] nodeName = {"A", "B", "C", "D", "E", "F", "G"};
        Graph graph = new Graph(7, nodeName);
        System.out.println("最短路径为: " + prim(graph));
    }

    private static int prim(Graph graph) {
        int ans = 0;
        HashSet<String> set = new HashSet<>(graph.node);
        while (!set.isEmpty()) {
            int minValue = 10000;
            int[] minIndex = new int[2];
            for (int i = 0; i < graph.edges.length; i++) {
                for (int j = 0; j < graph.edges[i].length; j++) {
                    // 除了第一次，下一个节点必须是连在之前存在的节点上
                    if (ans != 0) {
                        if ((!set.contains(graph.node.get(i)) || set.contains(graph.node.get(j)) && (!set.contains(graph.node.get(j)) || set.contains(graph.node.get(i))))) {
                            continue;
                        }
                    }
                    // 找最小值
                    if (graph.edges[i][j] != 0 && graph.edges[i][j] < minValue) {
                        minIndex[0] = i;
                        minIndex[1] = j;
                        minValue = graph.edges[i][j];
                    }
                }
            }
            graph.add(minIndex[0], minIndex[1], 0);
            set.remove(graph.node.get(minIndex[0]));
            set.remove(graph.node.get(minIndex[1]));
            ans += minValue;
        }
        return ans;
    }
}

class Graph {
    int[][] edges;  // 邻接矩阵
    int n;  // 节点个数
    List<String> node;  // 节点名称

    public Graph(int n, String[] nodeName) {
        this.edges = new int[n][n];
        this.n = n;
        this.node = new ArrayList<>(Arrays.asList(nodeName));
        this.init();
    }

    private void init() {
        /*
            "A"     0
            "B"     1
            "C"     2
            "D"     3
            "E"     4
            "F"     5
            "G"     6
         */
        // A-B:5    A-C:7   A-G:2
        add(0, 1, 5).add(0, 2, 7).add(0, 6, 2);
        // F-E:5    F-D:4   F-G:6
        add(5, 4, 5).add(5, 3, 4).add(5, 6, 6);
        // E-G:4    E-C:8
        add(4, 6, 4).add(4, 2, 8);
        // B-D:9    B-G:3
        add(1, 3, 9).add(1, 6, 3);
    }

    public Graph add(int i, int j, int weight) {
        edges[i][j] = edges[j][i] = weight;
        return this;
    }
}

八、迪杰斯特拉算法（Dijkstra）

1、最短路径问题

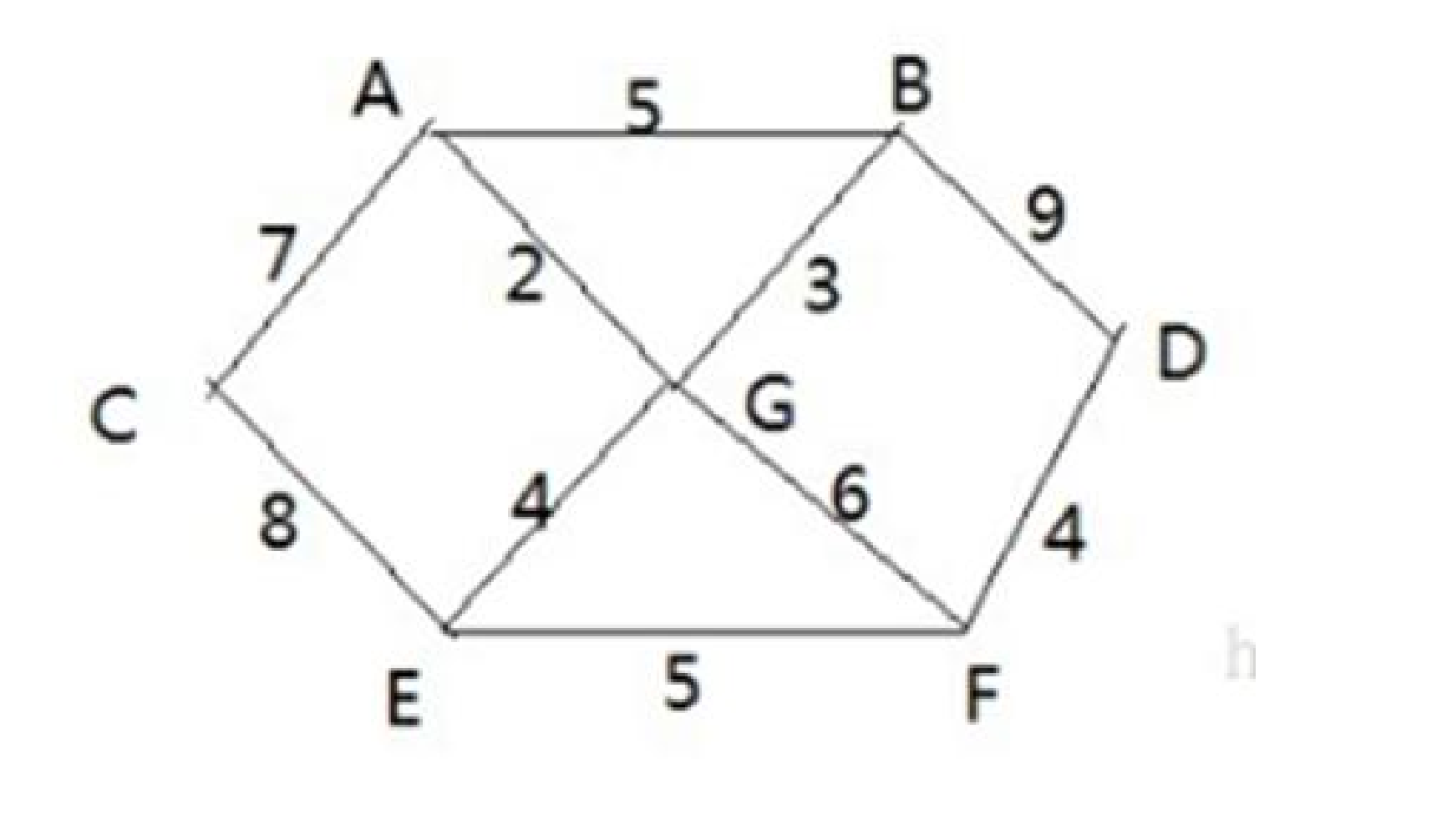
最短路径问题

如何计算出 G 村庄到其它各个村庄的最短距离?

2、迪杰斯特拉算法概要

迪杰斯特拉(Dijkstra)算法是典型最短路径算法，用于计算一个结点到其他结点的最短路径。它的主要特点是以起始点为中心向外层层扩展（广度优先搜索思想），直到扩展到终点为止。

3、迪杰斯特拉算法基本思想

每次从未标记的节点中选择距离出发点最近的节点，标记，收录到最优路径集合中。
计算刚加入节点A的邻近节点B的距离（不包含标记的节点），若（节点A的距离＋节点A到节点B的边长）＜节点B的距离，就更新节点B的距离和前面点。

4、迪杰斯特拉算法代码实现

java

package work.rexhao.algorithm.dijkstra;

import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;

/**
 * 迪杰斯特拉算法
 *
 * @author 王铭颢
 * @Date 2022/7/15 01:15
 */
public class DijkstraAlgorithm {

    public static void main(String[] args) {
        // 数据初始化
        String[] nodeName = {"A", "B", "C", "D", "E", "F", "G"};
        DijkstraForm[] df = new DijkstraForm[7];
        for (int i = 0; i < 7; i++) {
            df[i] = new DijkstraForm(i);
        }
        Graph graph = new Graph(7, nodeName);

        // 调用dijkstra方法
        df[6].pre = 6;
        df[6].len = 0;
        dijkstra(df, graph, nodeName, 6);   //G

        // 格式化输出
        for (int i = 0; i < 7; i++) {
            System.out.println("G --> " + nodeName[i] + " : " + "len = " + df[i].len + " , pre = " + nodeName[df[i].pre]);
        }
    }

    public static void dijkstra(DijkstraForm[] df, Graph graph, String[] nodeName, int i) {
        // 1. 判结束
        boolean flag = true;
        for (DijkstraForm dijkstraForm : df) {
            if (!dijkstraForm.flag) {
                flag = false;
                break;
            }
        }
        if (flag) return;

        // 2. 标记自己
        df[i].flag = true;

        // 3. 更新相邻的表
        for (int j = 0; j < graph.edges.length; j++) {
            if (graph.edges[i][j] != 0 && !df[j].flag
                    && graph.edges[i][j] + df[i].len < df[j].len) {
                df[j].len = graph.edges[i][j] + df[i].len;
                df[j].pre = i;
            }
        }

        // 4. 递归最小的相邻表
        int minValue = 10000;
        int minIndex = -1;
        for (int j = 0; j < df.length; j++) {
            if (df[j].flag) continue;
            if (minValue > df[j].len) {
                minIndex = j;
                minValue = df[j].len;
            }
        }
        dijkstra(df, graph, nodeName, minIndex);
    }

}

class DijkstraForm {
    int n;
    int pre;
    int len;    // 路径长度
    boolean flag;   //  标记

    public DijkstraForm(int n) {
        this.n = n;
        this.len = 100000;
        this.flag = false;
    }
}

class Graph {
    int[][] edges;  // 邻接矩阵
    int n;  // 节点个数
    List<String> node;  // 节点名称

    public Graph(int n, String[] nodeName) {
        this.edges = new int[n][n];
        this.n = n;
        this.node = new ArrayList<>(Arrays.asList(nodeName));
        this.init();
    }

    private void init() {
        /*
            "A"     0
            "B"     1
            "C"     2
            "D"     3
            "E"     4
            "F"     5
            "G"     6
         */
        // A-B:5    A-C:7   A-G:2
        add(0, 1, 5).add(0, 2, 7).add(0, 6, 2);
        // F-E:5    F-D:4   F-G:6
        add(5, 4, 5).add(5, 3, 4).add(5, 6, 6);
        // E-G:4    E-C:8
        add(4, 6, 4).add(4, 2, 8);
        // B-D:9    B-G:3
        add(1, 3, 9).add(1, 6, 3);
    }

    public Graph add(int i, int j, int weight) {
        edges[i][j] = edges[j][i] = weight;
        return this;
    }
}

G --> A : len = 2 , pre = G G --> B : len = 3 , pre = G G --> C : len = 9 , pre = A G --> D : len = 10 , pre = F G --> E : len = 4 , pre = G G --> F : len = 6 , pre = G G --> G : len = 0 , pre = G

九、弗洛伊德算法（Floyd）

1、弗洛伊德算法介绍

和 Dijkstra 算法一样，弗洛伊德(Floyd)算法也是一种用于寻找给定的加权图中顶点间最短路径的算法。该算法名称以创始人之一、1978 年图灵奖获得者、斯坦福大学计算机科学系教授罗伯特·弗洛伊德命名

弗洛伊德算法 VS 迪杰斯特拉算法：
迪杰斯特拉算法通过选定的被访问顶点，求出从出发访问顶点到其他顶点的最短路径。
弗洛伊德算法中每一个顶点都是出发访问点，所以需要将每一个顶点看做被访问顶点，求出从每一个顶点到其他顶点的最短路径。

2、弗洛伊德算法思路分析

设置顶点 vi 到顶点 vk 的最短路径已知为 Lik，顶点 vk 到 vj 的最短路径已知为 Lkj，顶点 vi 到 vj 的路径为 Lij，则 vi 到 vj 的最短路径为：min((Lik+Lkj),Lij)，vk 的取值为图中所有顶点，则可获得 vi 到 vj 的最短路径
至于 vi 到 vk 的最短路径 Lik 或者 vk 到 vj 的最短路径 Lkj，是以同样的方式获得

3、弗洛伊德算法代码实现

java

package work.rexhao.algorithm.floyd;

import java.util.*;

/**
 * 弗洛伊德算法
 *
 * @author 王铭颢
 * @Date 2022/7/15 10:50
 */
public class FloydAlgorithm {
    static int[][] len;
    static int[][] pre;

    public static void main(String[] args) {
        String[] nodeName = {"A", "B", "C", "D", "E", "F", "G"};
        Graph graph = new Graph(7, nodeName);

        floyd(graph);
    }

    public static void floyd(Graph graph) {
        // 1. 对len表进行初始化
        len = new int[graph.n][graph.n];
        for (int i = 0; i < graph.n; i++) {
            for (int j = 0; j < graph.n; j++) {
                if (i == j) {
                    len[i][j] = 0;
                } else if (graph.edges[i][j] != 0) {
                    len[i][j] = graph.edges[i][j];
                } else {
                    len[i][j] = 10000;
                }
            }
        }
        // 2. 对pre表初始化
        pre = new int[graph.n][graph.n];
        for (int i = 0; i < graph.n; i++) {
            for (int j = 0; j < graph.n; j++) {
                pre[i][j] = i;
            }
        }

        // 3. 弗洛伊德算法
        // 3.1 i : 中间节点
        for (int i = 0; i < graph.n; i++) {
            // 3.2 j : 起始节点
            for (int j = 0; j < graph.n; j++) {
                // 3.3 k : 目的节点
                for (int k = 0; k < graph.n; k++) {
                    int temp = len[j][i] + len[k][i];
                    if (temp < len[j][k]) {
                        len[j][k] = temp;
                        pre[j][k] = i;
                    }
                }
            }
        }

        // 4. 输出测试
        for (int[] ints : len) {
            System.out.println(Arrays.toString(ints));
        }
        System.out.println("-------------");
        for (int[] p : pre) {
            System.out.println(Arrays.toString(p));
        }
        System.out.println("-------------");
    }
}

class Graph {
    int[][] edges;  // 邻接矩阵
    int n;  // 节点个数
    List<String> node;  // 节点名称

    public Graph(int n, String[] nodeName) {
        this.edges = new int[n][n];
        this.n = n;
        this.node = new ArrayList<>(Arrays.asList(nodeName));
        this.init();
    }

    private void init() {
        /*
            "A"     0
            "B"     1
            "C"     2
            "D"     3
            "E"     4
            "F"     5
            "G"     6
         */
        // A-B:5    A-C:7   A-G:2
        add(0, 1, 5).add(0, 2, 7).add(0, 6, 2);
        // F-E:5    F-D:4   F-G:6
        add(5, 4, 5).add(5, 3, 4).add(5, 6, 6);
        // E-G:4    E-C:8
        add(4, 6, 4).add(4, 2, 8);
        // B-D:9    B-G:3
        add(1, 3, 9).add(1, 6, 3);
    }

    public Graph add(int i, int j, int weight) {
        edges[i][j] = edges[j][i] = weight;
        return this;
    }
}

十、马踏棋盘算法（DFS）

1、马踏棋盘介绍

将马随机放在国际象棋的8×8棋盘的某个方格中，马按走棋规则（马走日字）进行移动。要求每个方格只进入一次，走遍棋盘上全部64个方格

2、马踏棋盘问题的思路分析

创建棋盘map，是一个二维数组
将当前位蛋设蛋为已经访问，向8个方向中可以继续前进的方向上递归调用，如果走通，就继续；走不通，就回溯
判断马儿是否完成了任务，使用count和应该走的步数比较

3、马踏棋盘问题代码实现

java

package work.rexhao.algorithm.horse;


import java.util.Arrays;
import java.util.Date;

/**
 * 马踏棋盘问题
 *
 * @author 王铭颢
 * @Date 2022/7/15 11:29
 */
public class HorseChessboard {
    static int[][] dir = {{1, 2}, {1, -2}, {-1, 2}, {-1, -2}, {2, 1}, {2, -1}, {-2, 1}, {-2, -1}};
    static boolean[][] vis = new boolean[8][8];
    static int[][] map = new int[8][8];
    static boolean over;

    public static void main(String[] args) {
        Date date0 = new Date();
        long begin = date0.getTime();

        dfs(3, 3, 1);

        Date date1 = new Date();
        long end = date1.getTime();
        System.out.println("运行时间:" + (end - begin) + "ms"); //1100
        System.out.println("----------------");

        for (int[] ints : map) {
            System.out.println(Arrays.toString(ints));
        }
    }

    public static void dfs(int x, int y, int count) {
        if (over || count > 64) {
            return;
        }
        if (count == 64) {
            over = true;
            return;
        }
        vis[x][y] = true;
        map[x][y] = count;
        int tx, ty;
        for (int[] ints : dir) {
            tx = x + ints[0];
            ty = y + ints[1];
            if (ty >= 0 && tx >= 0 && ty < 8 && tx < 8 && !vis[tx][ty]) {
                dfs(tx, ty, count + 1);
            }
        }
        vis[x][y] = false;
    }
}

十大算法 ​

一、二分查找（非递归） ​

1、非递归二分查找概述 ​

2、非递归二分查找代码实现 ​

3、补：递归二分查找代码实现 ​

二、分治算法（DC） ​

1、分治算法介绍 ​

2、分治算法的基本步骤 ​

3、分治算法设计模式 ​

4、汉诺塔代码实现 ​

三、动态规划（DP） ​

1、动态规划算法介绍 ​

2、背包问题 ​

1）背包问题概述 ​

2）背包问题思路分析 ​

3）背包问题代码实现 ​

3、最少步数问题 ​

1）最少步数问题概述 ​

2）最少步数问题思路分析 ​

3）最少步数问题代码实现 ​

四、KMP算法 ​

1、字符串匹配问题 ​

2、暴力破解（BF）代码实现 ​

3、KMP介绍 ​

4、KMP思路分析 ​

5、KMP代码实现 ​

五、贪心算法 ​

1、贪心算法介绍 ​

2、集合覆盖问题 ​

3、集合覆盖问题代码实现 ​

六、普利姆算法（Prim） ​

1、最小生成树 ​

2、普利姆算法概要 ​

3、修路问题 ​

4、普利姆算法代码实现 ​

七、克鲁斯卡尔算法（Kruskal） ​

1、克鲁斯卡尔算法概要 ​

2、Kruskal与Prim的区别 ​

3、克鲁斯卡尔算法代码实现 ​

八、迪杰斯特拉算法（Dijkstra） ​

1、最短路径问题 ​

2、迪杰斯特拉算法概要 ​

3、迪杰斯特拉算法基本思想 ​

4、迪杰斯特拉算法代码实现 ​

九、弗洛伊德算法（Floyd） ​

1、弗洛伊德算法介绍 ​

2、弗洛伊德算法思路分析 ​

3、弗洛伊德算法代码实现 ​

十、马踏棋盘算法（DFS） ​

1、马踏棋盘介绍 ​

2、马踏棋盘问题的思路分析 ​

3、马踏棋盘问题代码实现 ​

十大算法

一、二分查找（非递归）

1、非递归二分查找概述

2、非递归二分查找代码实现

3、补：递归二分查找代码实现

二、分治算法（DC）

1、分治算法介绍

2、分治算法的基本步骤

3、分治算法设计模式

4、汉诺塔代码实现

三、动态规划（DP）

1、动态规划算法介绍

2、背包问题

1）背包问题概述

2）背包问题思路分析

3）背包问题代码实现

3、最少步数问题

1）最少步数问题概述

2）最少步数问题思路分析

3）最少步数问题代码实现

四、KMP算法

1、字符串匹配问题

2、暴力破解（BF）代码实现

3、KMP介绍

4、KMP思路分析

5、KMP代码实现

五、贪心算法

1、贪心算法介绍

2、集合覆盖问题

3、集合覆盖问题代码实现

六、普利姆算法（Prim）

1、最小生成树

2、普利姆算法概要

3、修路问题

4、普利姆算法代码实现

七、克鲁斯卡尔算法（Kruskal）

1、克鲁斯卡尔算法概要

2、Kruskal与Prim的区别

3、克鲁斯卡尔算法代码实现

八、迪杰斯特拉算法（Dijkstra）

1、最短路径问题

2、迪杰斯特拉算法概要

3、迪杰斯特拉算法基本思想

4、迪杰斯特拉算法代码实现

九、弗洛伊德算法（Floyd）

1、弗洛伊德算法介绍

2、弗洛伊德算法思路分析

3、弗洛伊德算法代码实现

十、马踏棋盘算法（DFS）

1、马踏棋盘介绍

2、马踏棋盘问题的思路分析

3、马踏棋盘问题代码实现