编程好记

主题

全连接神经网络 ​

全连接神经网络的结构 ​

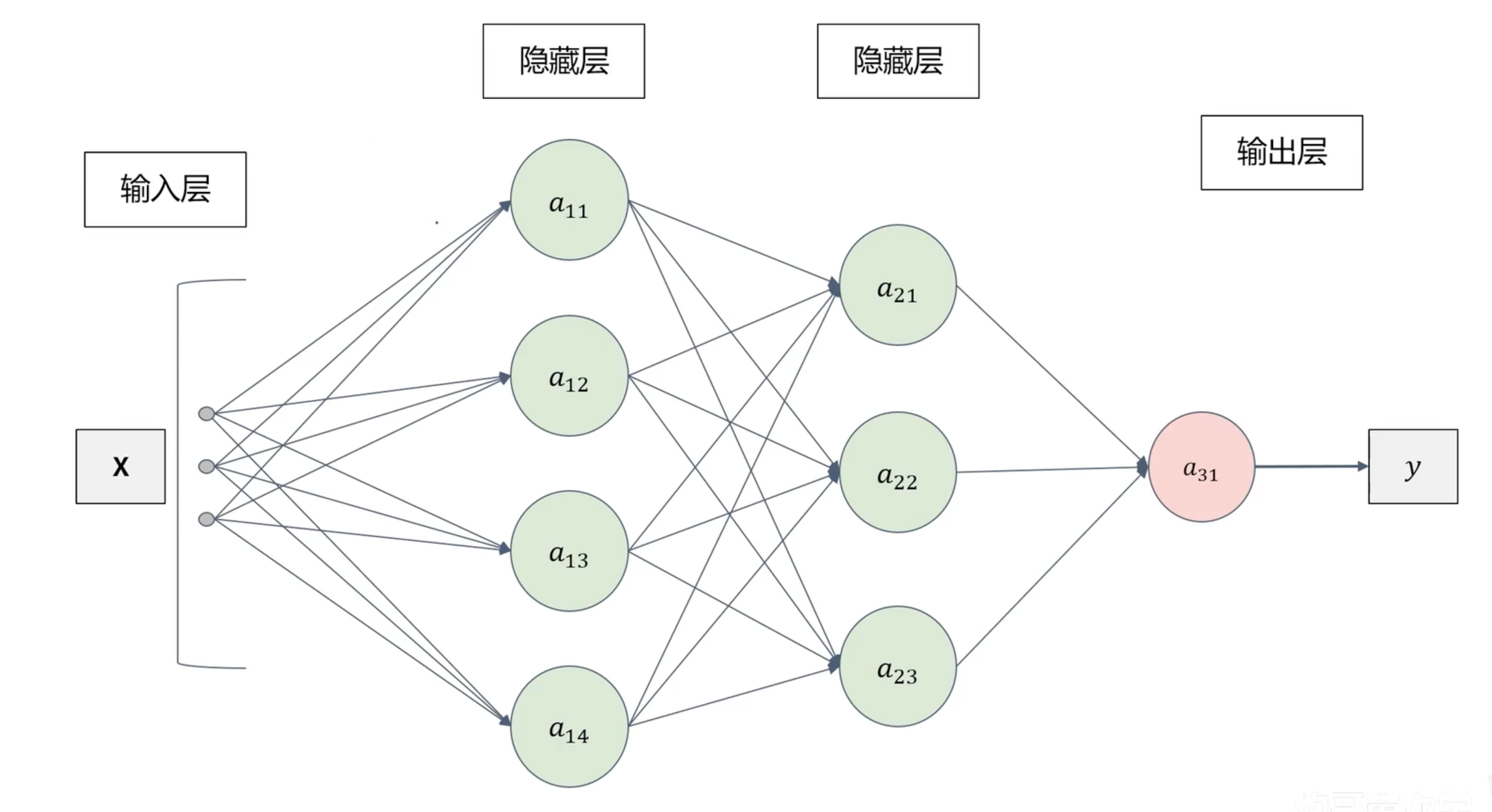
整体结构 ​

神经网络：类似神经元，前一层可以不断地传递给下一层。

神经网络模型由多个单元结构组成。

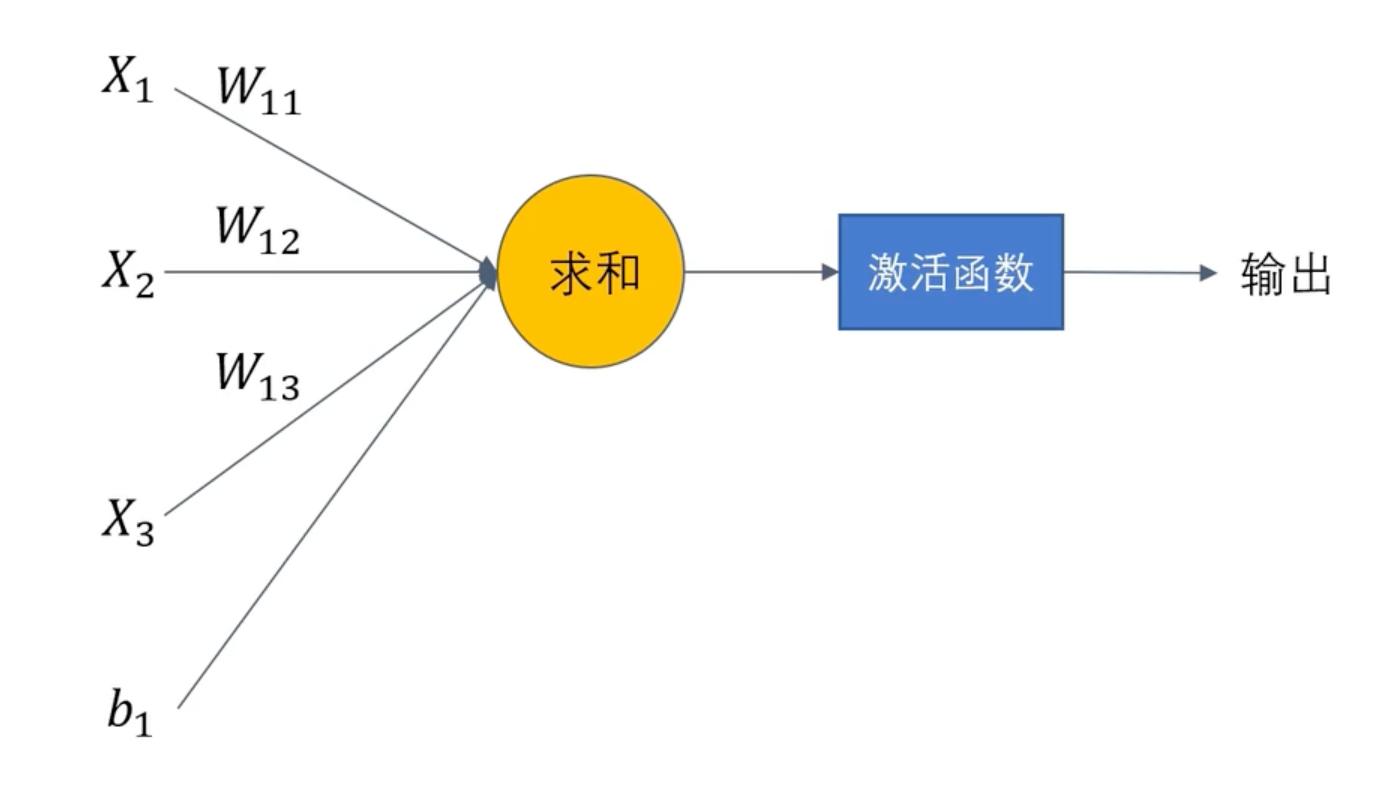
单元结构 ​

单元结构的数学公式：a=h(wx+b)a=h(wx+b)

h(x)：激活函数

  • 比如sigmoid就是激活函数之一
  • 隐藏层大多需要激活函数

image-20240124144525163

激活函数 ​

激活函数概述 ​

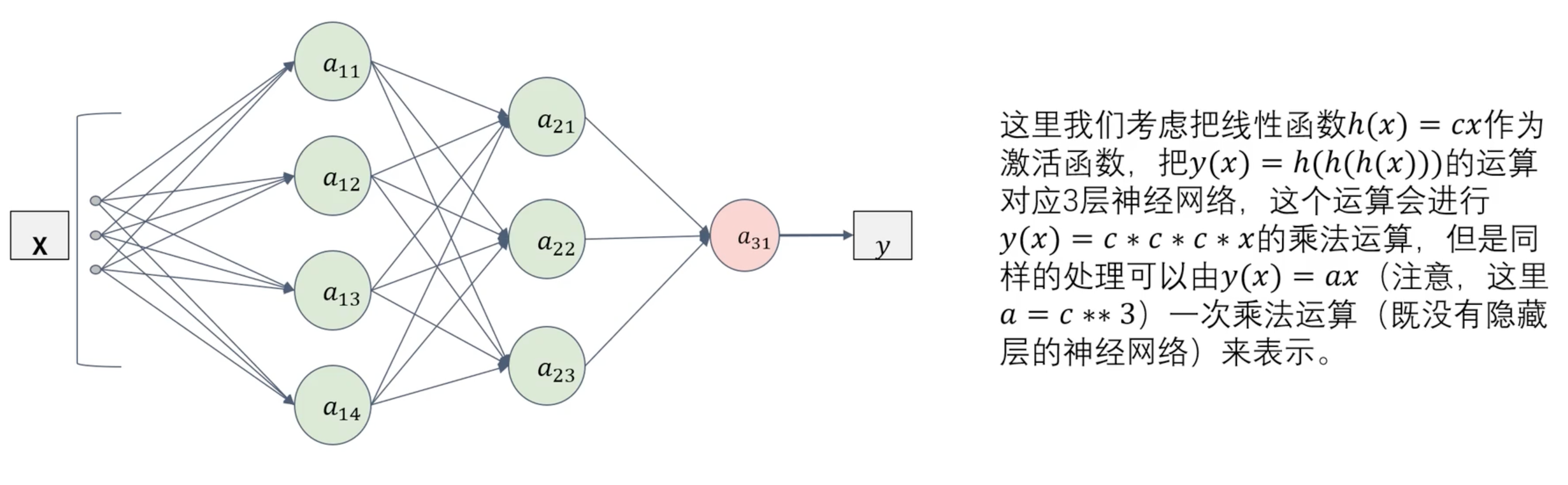
激活函数是非线性的函数（图像不是直线的）。

非线性激活函数引入了非线性变换，使得神经网络可以逼近任意复杂的函数，从而更好地完成分类、回归和其他任务。增加神经网络的表达能力，使其能够学习和表示更加复杂的模式和关系。

激活函数必须是非线性的，因为如果激活函数是线性的话，无论神经网络有多少层，整个网络都可以被简化为单层网络。 a31=kx;k=c3a_{31}=kx; k=c^3 和 a11=cxa_{11}=cx 都是线性回归。

Sigmoid函数 ​

函数公式和导数：

image-20240124151934848

函数及其导数图像：

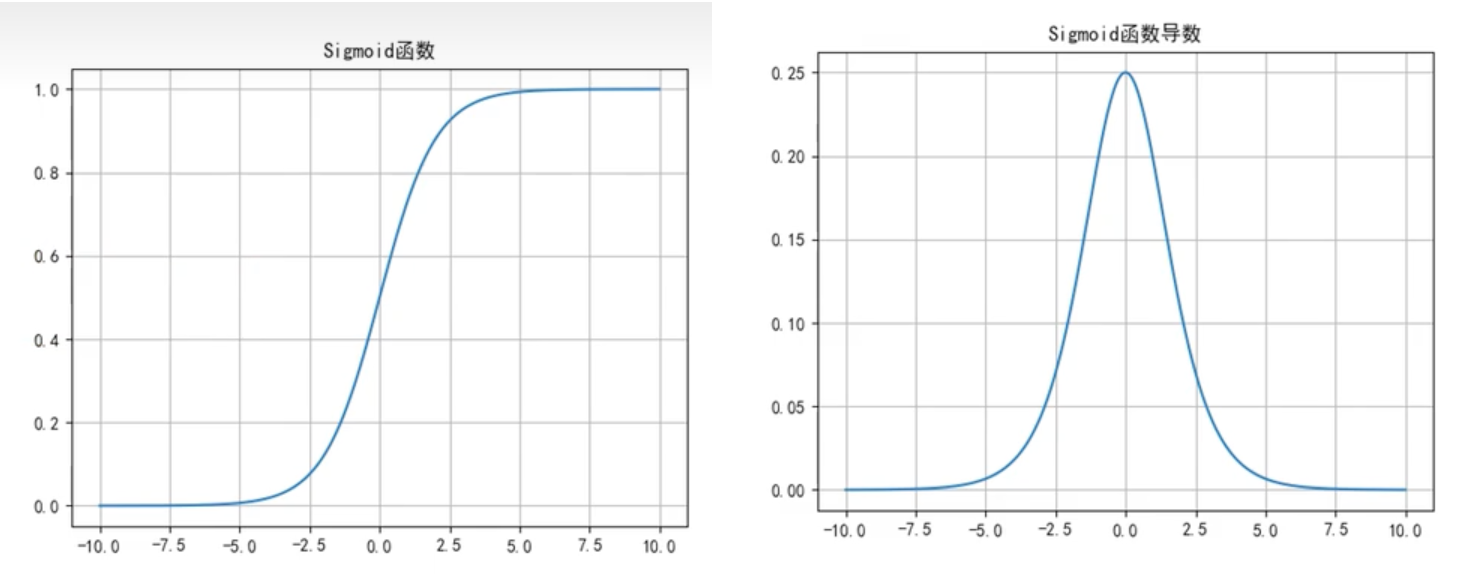
Sigmoid函数优点：简单、非常适用分类任务；

Sigmoid函数缺点：

  1. 反向传播训练时有梯度消失的问题；
  2. 输出值区间为(0,1)，关于0不对称；
  3. 梯度更新在不同方向走得太远，使得优化难度增大，训练耗时。

Tanh函数 ​

函数公式和导数：

image-20240124154749778

函数及其导数图像：

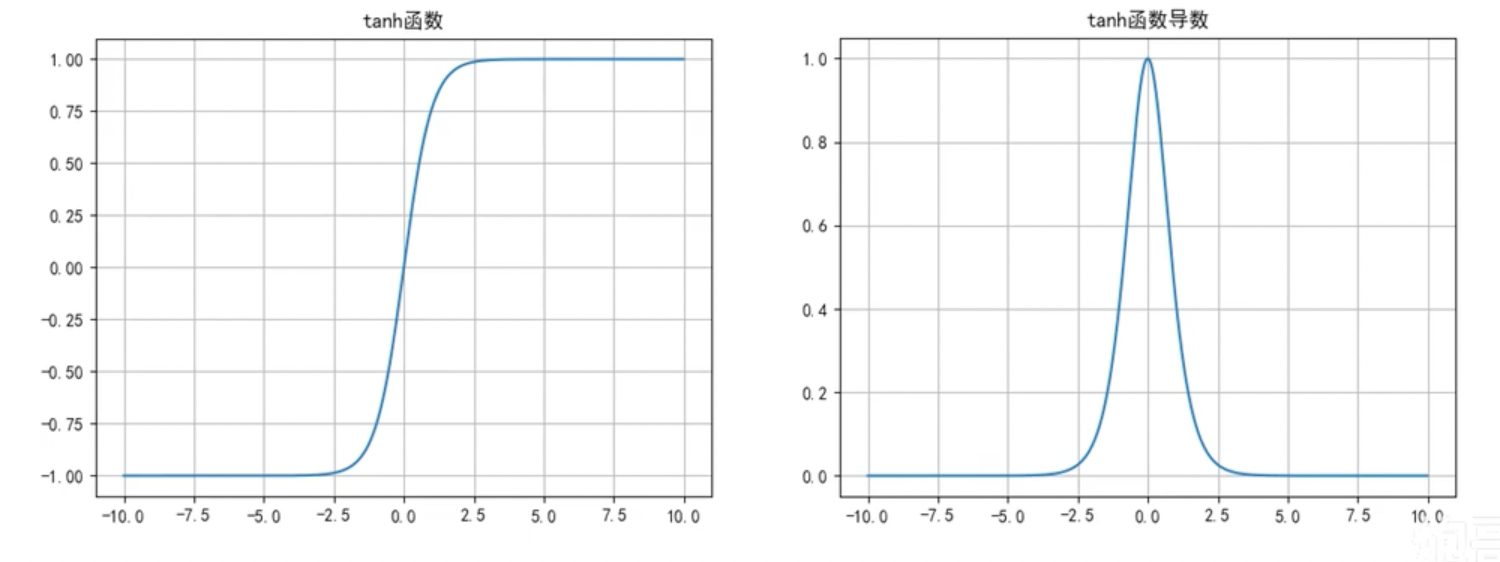
Tanh函数优点：

  1. 解决了Sigmoid函数输出值非0对称的问题，
  2. 训练比Sigmoid函数快，更容易收敛；

Tanh函数缺点：

  1. 反向传播训练时有梯度消失的问题，
  2. Tanh函数和Sigmoid函数非常相似。

ReLU函数 ​

函数公式和导数：

image-20240124155329732

函数及其导数图像：

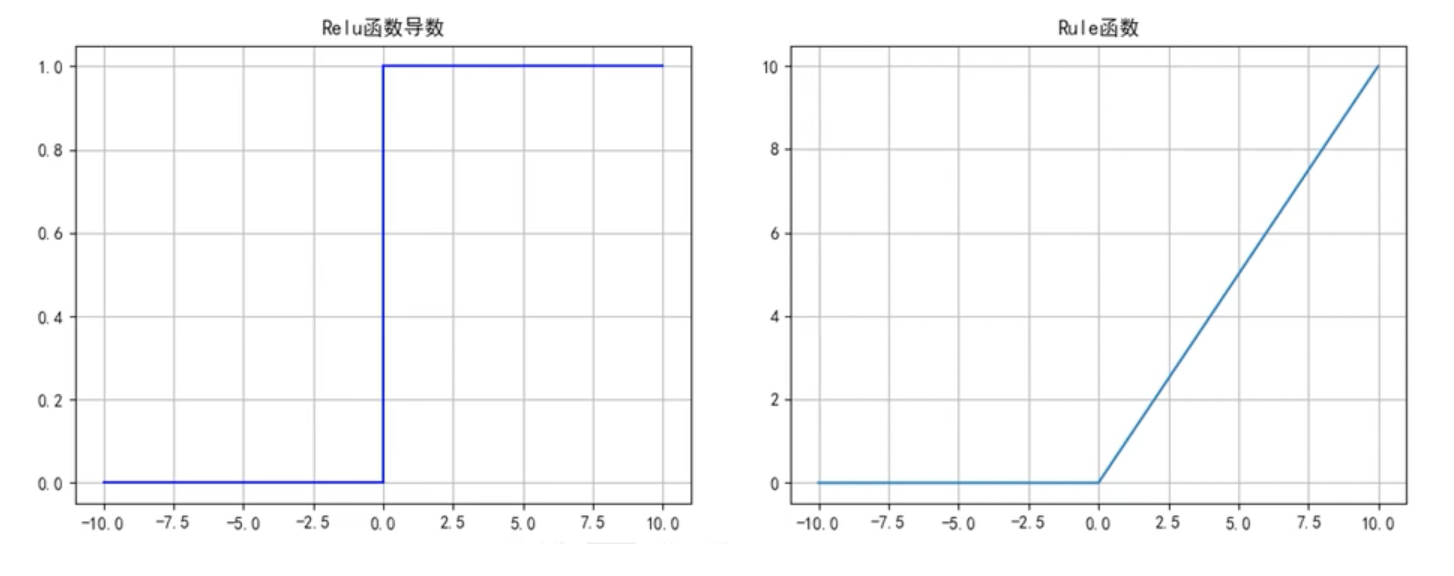
ReLU函数优点：

  1. 解决了梯度消失的问题；
  2. 计算更为简单，没有Sigmoid函数和Tanh函数的指数运算；

ReLU函数缺点：

  1. 训练时可能出现神经元死亡（损失函数导数为0，无法更新参数）
  2. 不关于原点对称

Leaky ReLU函数 ​

函数公式和导数：

image-20240124155848852

函数及其导数图像：

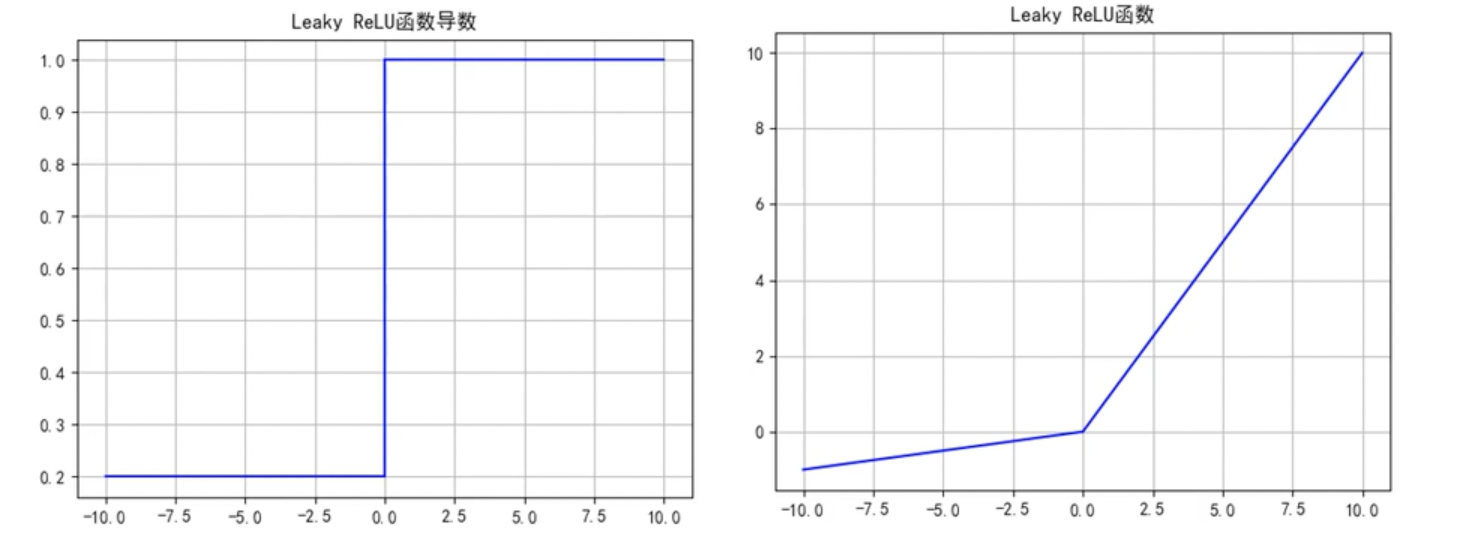
Leaky ReLU函数优点：解决了ReLU的神经元死亡问题；

Leaky ReLU函数缺点：无法为正负输入值提供一致的关系预测（不同区间函数不同)

当输入是正数时，神经元的输出会受到一个比较大的斜率的影响，而当输入是负数时，神经元的输出会受到一个比较小的斜率的影响。这种情况下，神经元对于正数和负数的处理方式不同，可能会导致模型学习到不一致的特征表示，从而影响模型的性能。

SoftMax函数 ​

函数公式和导数：

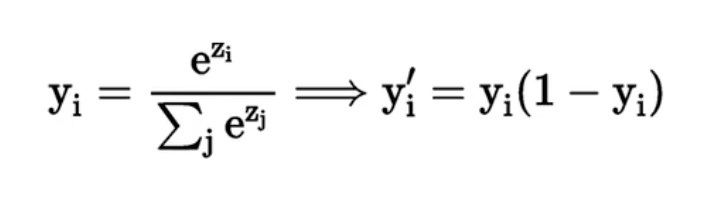
image-20240124173214725

SoftMax函数常常作为输出层，用于多分类。

前向传播 ​

前向传播：模型推理的过程。

将输入数据通过网络层层传递，最终得到输出结果的过程。

已知w、b，通过 x 求 y 的过程

前向传播计算过程：

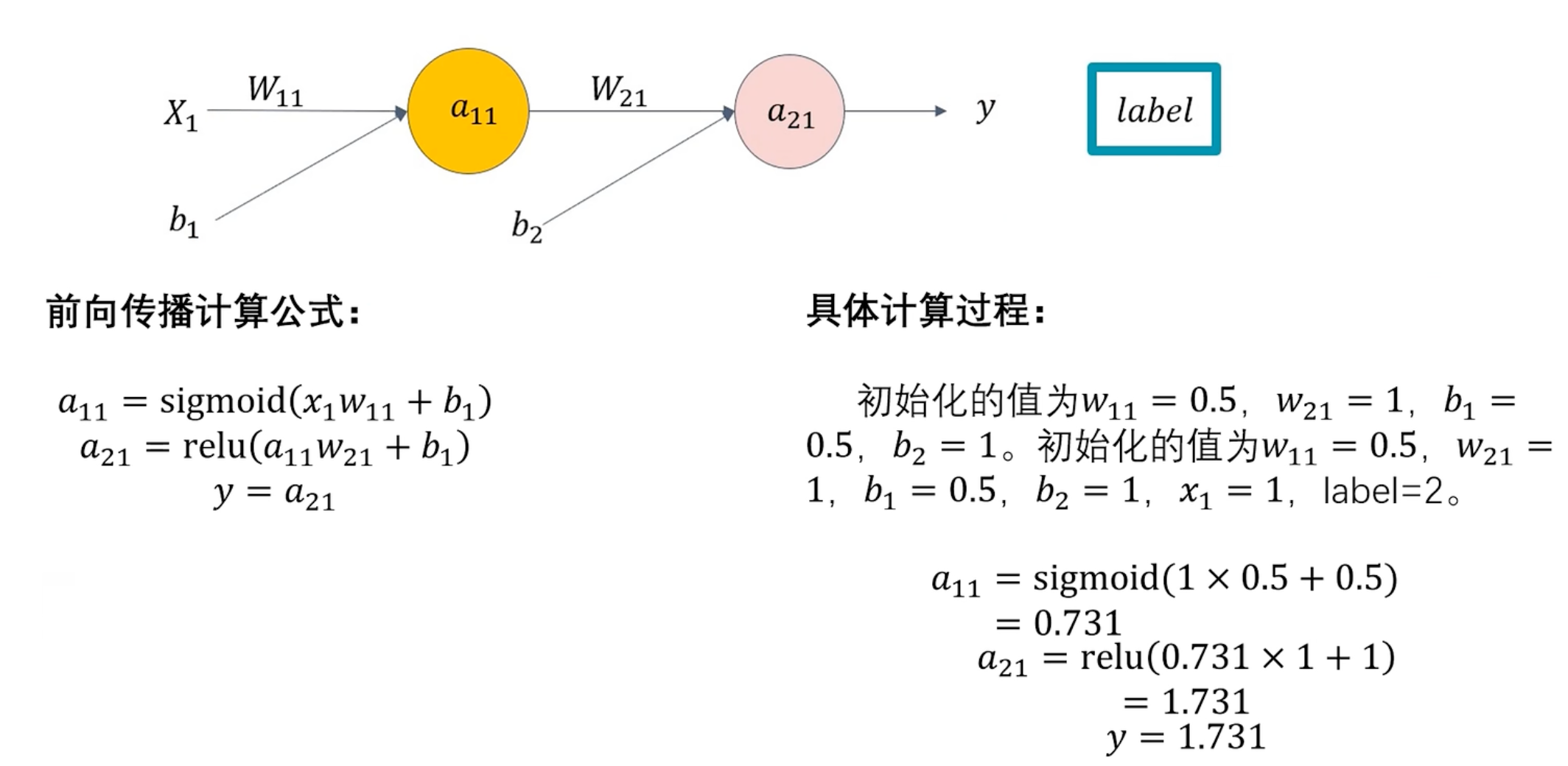
数据会被划分三类：

  1. 训练集
  2. 验证集
  3. 测试集
  • 制作两份损失函数图像：训练集损失图和验证集损失图，避免产生过拟合。

链式求导法则 ​

单变量链式法则定义：

image-20240124195054265

单变量链式法则算例：

image-20240124195832368

多变量链式法则定义：

求偏导：把无关项当成常量，两次求导相加。

image-20240124195552267

多变量链式法则算例：

image-20240124195906754

反向传播 ​

反向传播：通过损失函数和梯度下降求得w、b的过程。

神经网络学习的过程：

  1. 划分数据集（csv → X/Y → x/y_train/test）
  2. 选择模型
  3. 前向传播（计算推理值）
  4. 计算误差（计算推理值和真实值的差距）
  5. 计算梯度（计算损失函数对于每个参数的变化率/导数值）
  6. 反向传播（利用梯度下降更新参数）
  7. 设置学习轮次
  8. 导出模型
  9. 应用模型

分类检测代码实现 ​

导入依赖 ​

python
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

# 归一化
from sklearn.preprocessing import MinMaxScaler
# 划分数据集
from sklearn.model_selection import train_test_split
# 计算评价指标
from sklearn.metrics import classification_report

import keras
# 创建全连接层(稠密层)
from keras.layers import Dense
# 转换"独热编码"
from keras.utils import to_categorical

# 解决中文显示问题
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

数据预处理 ​

独热编码：将多分类任务转化为独热向量，减小不同分类直接的影响。

python
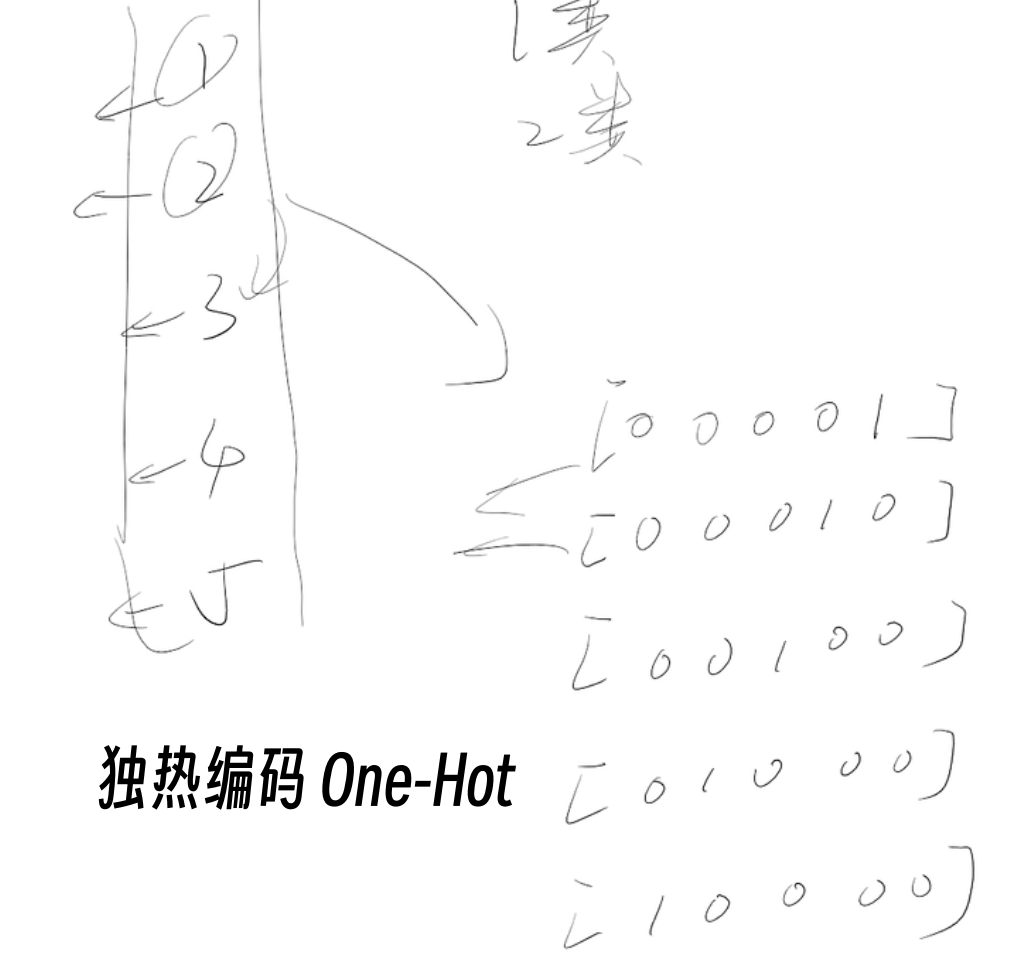
# 加载数据集
dataset = pd.read_csv("../heart_disease.csv")

# 划分数据集
X = dataset.iloc[:, :-1]
Y = dataset['target']
# 将特征规归一化
sc = MinMaxScaler(feature_range=(0, 1))
X = sc.fit_transform(X)
# 将标签转化为独热向量
Y = to_categorical(Y, 2)
# 划分测试集和训练集
x_train, x_test, y_train, y_test = train_test_split(X, Y, test_size=.2, random_state=114514)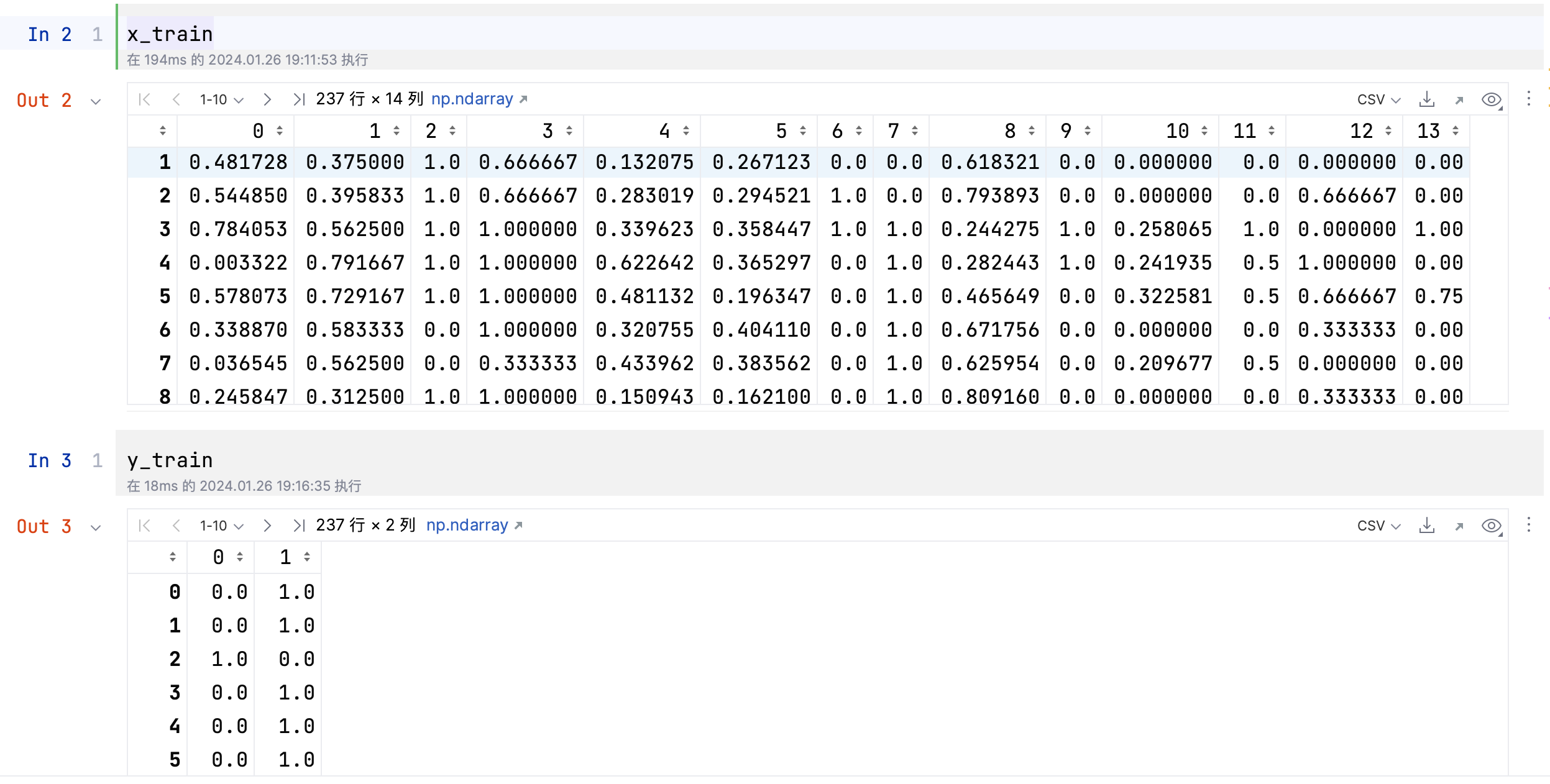
image-20240126191737047

模型训练 ​

python
# 利用Keras搭建模型
model = keras.Sequential()
# 隐藏层第一层
model.add(Dense(10, activation='relu'))
# 隐藏层第二层
model.add(Dense(10, activation='relu'))
# 二分类 -> 输出两个神经元
model.add(Dense(2, activation='softmax'))

# 编译模型
# loss损失函数: 交叉熵
# optimizer优化器: 优化模型参数
# metrics评估指标: 评估模型性能
model.compile(loss="categorical_crossentropy", optimizer="SGD", 
              metrics=["accuracy"])

# 模型训练
# validation_data: 验证集
# verbose: 显示训练过程
his = model.fit(x_train, y_train, epochs=100, batch_size=16,
                validation_data=(x_test, y_test), verbose=2)

# 保存模型
timestamp = datetime.datetime.now().strftime('%Y-%m-%d-%H:%M:%S')
os.makedirs(f"./log_{timestamp}")
model.save(f"./log_{timestamp}/model.keras")

# loss对比图
plt.plot(his.history['loss'], 'b', label='训练集损失')
plt.plot(his.history['val_loss'], 'r', label='验证集损失')
plt.legend()
plt.savefig(f"./log_{timestamp}/loss.png")
plt.show()

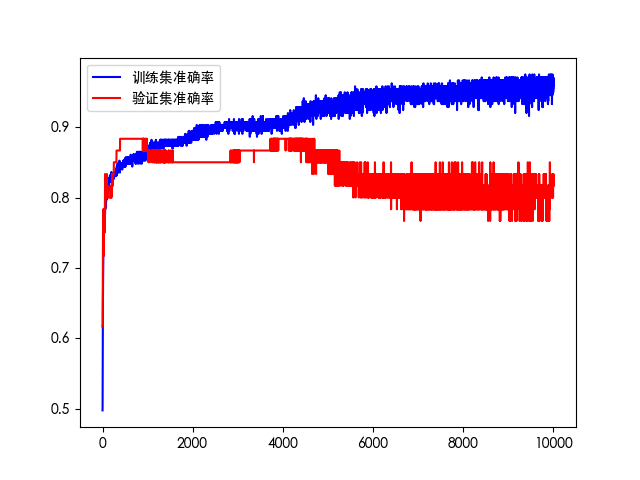
# 准确率对比图
plt.plot(his.history['accuracy'], 'b', label='训练集准确率')
plt.plot(his.history['val_accuracy'], 'r', label='验证集准确率')
plt.legend()
plt.savefig(f"./log_{timestamp}/accuracy.png")
plt.show()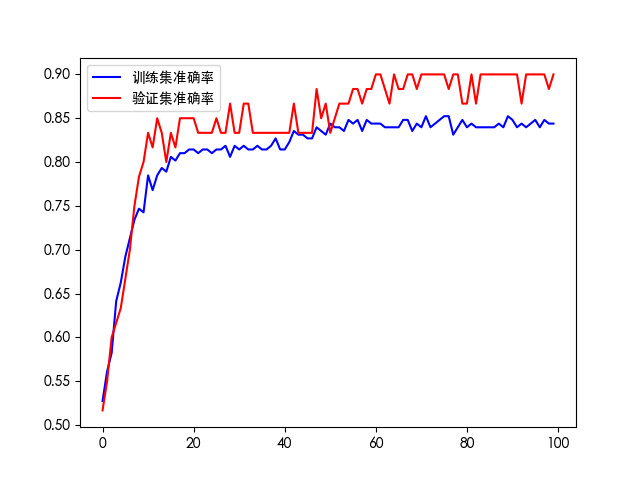
accuracyloss

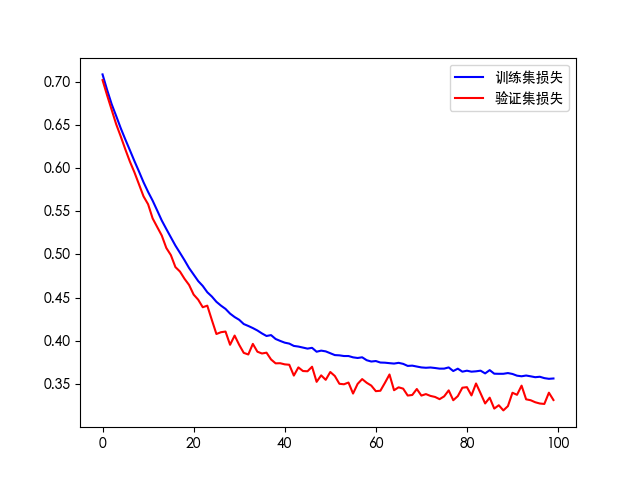
如果训练轮次过多会出现过拟合现象。

image-20240126202129867

模型预测 ​

python
# 加载数据集
dataset = pd.read_csv("../heart_disease.csv")

# 划分数据集
X = dataset.iloc[:, :-1]
Y = dataset['target']
# 将特征规归一化
sc = MinMaxScaler(feature_range=(0, 1))
X = sc.fit_transform(X)
# 划分测试集和训练集
_, x_test, _, y_test = train_test_split(X, Y, test_size=.2, random_state=114514)

# 导入模型
model = keras.models.load_model("./log_2024-01-26-20:12:37/model.h5")

# 推演
pre_test = model.predict(x_test)

# 将预测结果转化为0，1
# axis: 0表示按列处理，1表示按行处理
pre_test = np.argmax(pre_test, axis=1)

# 计算准确率
check = 0
for i, j in zip(pre_test, y_test.values):
    if i == j:
        check += 1
print(f"准确率: {check / len(pre_test) * 100 : .5f}%")

# 评估模型
report = classification_report(y_test, pre_test)
print(report)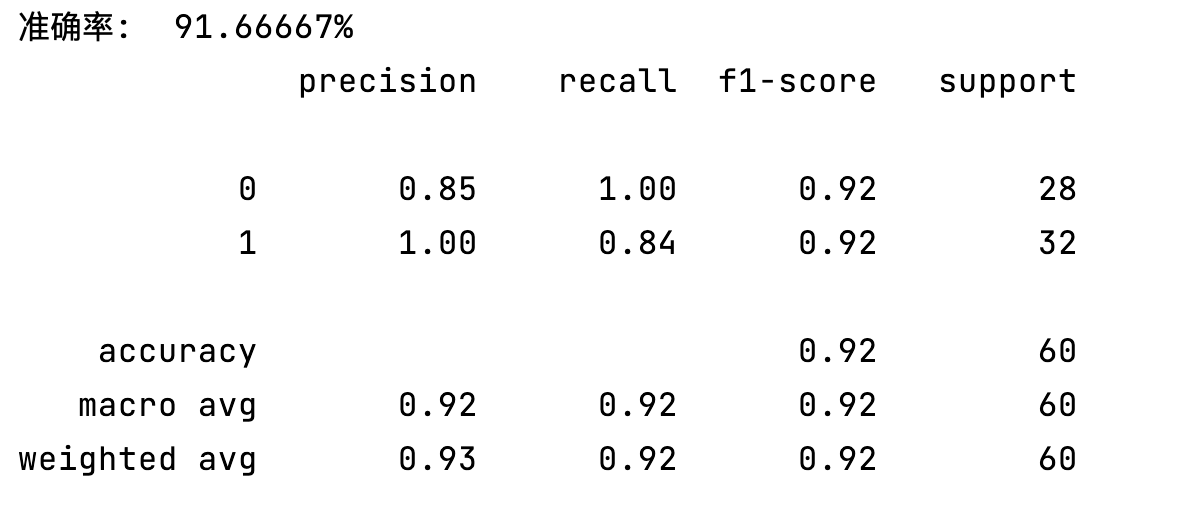

image-20240126202056257

回归预测代码实现 ​

损失函数的选择：

  1. 分类模型：交叉熵
  2. 回归模型：均方误差

模型训练 ​

这里没有找到合适数据，成功率较低。仅供参考思路。

python
import datetime
import os
import pandas as pd
import matplotlib.pyplot as plt
# 归一化
from sklearn.preprocessing import MinMaxScaler
# 划分数据集
from sklearn.model_selection import train_test_split
import keras
# 创建全连接层(稠密层)
from keras.layers import Dense

# 解决中文显示问题
plt.rcParams['font.sans-serif'] = ['Heiti TC']
plt.rcParams['axes.unicode_minus'] = False

# 加载数据集
dataset = pd.read_csv("../heart_disease_age.csv")
# 将特征与标签归一化
sc = MinMaxScaler(feature_range=(0, 1))
dataset = sc.fit_transform(dataset)
# 格式转换
dataset = pd.DataFrame(dataset)
# 划分数据集
X = dataset.iloc[:, :-1]
Y = dataset.iloc[:, -1]

# 划分测试集和训练集
x_train, x_test, y_train, y_test = train_test_split(X, Y, test_size=.2,
                                                    random_state=123)

# 利用Keras搭建模型
model = keras.Sequential()
# 隐藏层第一层
model.add(Dense(10, activation='relu'))
# 隐藏层第二层
model.add(Dense(10, activation='relu'))
# 输出层：不使用激活函数
model.add(Dense(1))

# 编译模型
# loss损失函数: 均方误差
# optimizer优化器: 优化模型参数
# metrics评估指标: 评估模型性能
model.compile(loss="mse", optimizer="SGD")

# 模型训练
# validation_data: 验证集
# verbose: 显示训练过程
his = model.fit(x_train, y_train, epochs=200, batch_size=8,
                validation_data=(x_test, y_test), verbose=2)

# 保存模型
timestamp = datetime.datetime.now().strftime('%Y-%m-%d-%H:%M:%S')
os.makedirs(f"./log_{timestamp}")
model.save(f"./log_{timestamp}/model.h5")

# loss对比图
plt.plot(his.history['loss'], 'b', label='训练集损失')
plt.plot(his.history['val_loss'], 'r', label='验证集损失')
plt.title(f"loss-{timestamp}")
plt.legend()
plt.savefig(f"./log_{timestamp}/loss.png")
plt.show()

模型预测 ​

反归一化：需要将归一化过的特征和标签合并后反归一化，

python
import keras
import numpy as np
import pandas as pd
# 划分数据集
from sklearn.model_selection import train_test_split
# 归一化
from sklearn.preprocessing import MinMaxScaler

# 加载数据集
dataset = pd.read_csv("../heart_disease_age.csv")
# 将特征与标签归一化
sc = MinMaxScaler(feature_range=(0, 1))
dataset = sc.fit_transform(dataset)
# 格式转换
dataset = pd.DataFrame(dataset)
# 划分数据集
X = dataset.iloc[:, :-1]
Y = dataset.iloc[:, -1]

# 划分测试集和训练集
x_train, x_test, y_train, y_test = train_test_split(X, Y, test_size=.2,
                                                    random_state=123)

# 导入模型
model = keras.models.load_model("./log_2024-02-01-22:54:44/model.h5")

# 推演
pre_value = model.predict(x_test)

# 合并数据
test_data = np.concatenate((x_test, pre_value), axis=1)
# 反归一化
test_data = sc.inverse_transform(test_data)
# 提取标签列
y_pre = test_data[:, -1]

评估模型 ​

  • 均方根误差（RMSE）
  • MAPE
python
# 计算rmse和mape
from sklearn.metrics import mean_squared_error
print("rmse:", mean_squared_error(y_test, y_pre))
print("mape:", np.mean(np.abs((y_test - y_pre) / y_test)))

# 画出真实值和预测值对比图
import matplotlib.pyplot as plt
# 解决中文显示问题
plt.rcParams['font.sans-serif'] = ['Heiti TC']
plt.rcParams['axes.unicode_minus'] = False
plt.plot(np.array(y_test), label="真实值")
plt.plot(pre_value, label="预测值")
plt.legend()
plt.show()
image-20240201231551983

​

Released under the MIT License.

code by wmh1024